Desigualdades Lineales:
Según el Criterio A, que es el que califica la Teoría:
Ya conoces los símbolos “>” (mayor que), “<” (menor que), “≥” (mayor o igual que) y  “≤” (menor o igual que)
Escribimos, por ejemplo, 4 >–1 para señalar que 4 es mayor que –1. También podemos escribir –2 < 3 para señalar que –2 es menor que 3.
Estos se conocen como desigualdades.
Ya sabiendo esto, diremos que una desigualdad es el enunciado que incluye alguna de las siguientes relaciones de orden: “mayor que”(>);  “menor que”  (<);  “mayor o igual que” (≥), y “menor o igual que” (≤). En la desigualdad aparece al menos un valor desconocido.
Si el grado (el numero de variables)de la desigualdad es uno (de primer grado), se dice que la inecuación es lineal.
Esto porque al escribir las desigualdades usamos números y por esto mismo es que podemos usar la recta numérica para graficar dichas desigualdades.  

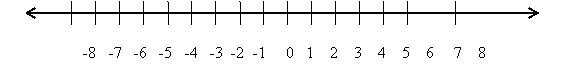
Observa que en la recta de arriba:

 4 > –1,  porque 4 está a la derecha de –1 en la recta numérica.

–2 < 3,  porque –2 está a la izquierda de 3 en la recta numérica

–3 < –1, porque -3 está a la izquierda de –1 en la recta numérica

 0 > –4, porque 0 está a la derecha de –4 en la recta numérica

 Una desigualdad lineal, entonces, es una expresión matemática que relaciona entre sí dos expresiones lineales.

Por ejemplo: 3 + 5x ≥ 18;  y otro, –2(x + 3) < –9.  

Ahora bien,  a la hora de resolver una ecuación lineal, el resultado queda como un intervalo (x,8),(x,9) etc. Si en la desigualdad, el simbolo se muestra como ≥ o ≤, quiere decir que el numero contiene. por ejemplo, si dice x≤5, quiere decir que el 5 es parte de la desigualdad, y en la gráfica se muestra así: 

 

Y, si el signo es  asi >, o asi <, quiere decir que el numero no contiene. Por ejemplo x<8, el 8 no esta en la comparación. 

Según el Criterio B, que es el que se encarga de calificar si el procedimiento está bien:
Como resolver una ecuación lineal (Simplificarla, Graficarla, y presentarla como un intervalo):
Resolución de inecuaciones lineales (de primer grado) con una incógnita
Veamos algunos ejemplos:
Resolver la inecuación 4x - 3 > 53 (Se resuelve exactamente como una ecuación, y el simbolo de mayor, menor o igual que, es como que si fuera un simbolo de = Ejemplo: 4x-3=53)

Tendremos:   4x − 3 + 3 > 53 + 3
                         4x > 53 +3
                         4x > 56
Tendremos ahora:     x > 56 ÷ 4
                                       x > 14
Entonces el valor de la incógnita o variable "x" serán todos los números mayores que 14, no incluyendo al 14.
Gráficamente, esta solución la representamos así:

Esto significa que en la recta numérica, desde el número 14 (sin incluirlo) hacia la derecha todos los valores (hasta el infinito + ∞) resuelven la inecuación.

Veamos el siguiente ejemplo:  –11x -5x +1 < –65x +36
Llevamos los términos semejantes a un lado de la desigualdad al otro lado de la desigualdad (hemos aplicado operaciones inversas donde era necesario).
–11x –5x +65x < 36 –1
Resolvemos las operaciones indicadas anteriormente
49x < 35
Aplicamos operaciones inversas, y simplificamos.

Y finalmente, buenas noticias:
El Criterio D es el que se encarga de calificar como usas una Desigualdad Lineal en la vida real, pero no hay aplicaciones en la vida real.